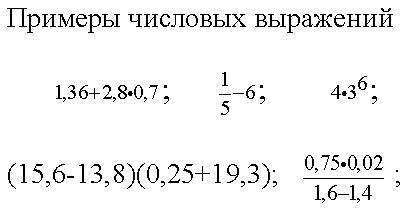Порядок выполнения арифметических действий

Порядок выполнения арифметических действий.

При нахождении значения числового выражения, мы должны соблюдать порядок выполнения арифметических действий. Его нужно запомнить раз и навсегда.



Если числовое выражение не содержит скобки, тогда порядок выполнения действий следующий:

1. Возведение в степень (например, возведение в квадрат или куб).
2. Умножение и деление.
3. Сложение и вычитание.

Арифметические действия одного типа выполняются в том порядке, в котором они следуют в выражении.

Если числовое выражение содержит скобки, то в первую очередь выполняются действия над числами, указанными в скобках. Причем порядок действий внутри скобок такой же, как для числового выражения без скобок.


Пример выполнения арифметических действий по порядку.

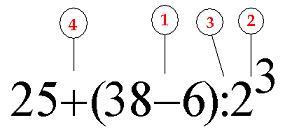
Итак, рассмотрим конкретный пример. Попробуем найти значение числового выражения:


Мы видим, что выражение содержит скобки, поэтому первым делом мы совершаем действия, указанные в скобках. 38-6=32. Получилось,


Теперь, когда у нас выражение уже без скобок, в первую очередь выполняем возведение в степень. ${{2}^{3}}=8$. Получаем,


Далее необходимо совершить деление. 32:8 = 4.

25+32:8 = 25+4.

Ну и наконец, осталось просто сложить оставшиеся числа. 25+4 = 29.

29 – значение числового выражения $25+(38-6):{{2}^{3}}$

Таким образом, следуя порядку выполнения арифметических действий, мы всегда легко сможем найти значение любого числового выражения. Этот процесс также называют алгоритмом нахождения числового выражения.
Хештеги: #алгебра :: #7 класс :: #порядок действий