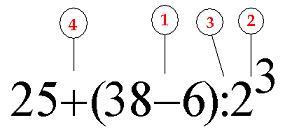
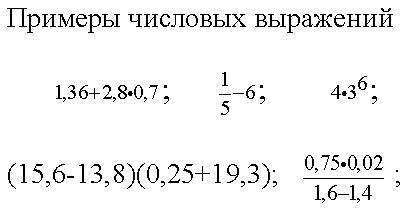Математическая модель

Математическая модель.

Математическая модель – это описание явления, закона, процесса или ситуации математическим языком.

Приведем пример реальной ситуации. В 7 классе ученикам приходится изучать на 3 предмета больше, чем в 6 классе. Как это записать математическим языком? Пусть количество изучаемых предметов в 6 классе будет X, а в 7 классе  - Y.

Тогда получается, что Y = X + 3. У нас получилась математическая модель реальной ситуации.



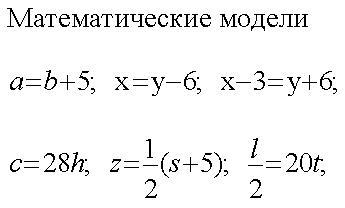
Примеры построения математической модели.

В одном мешке в 2 раза больше сахара, чем в другом. Пусть X кг сахара в первом мешке, а Y кг - во втором. Тогда X = 2Y.

Сегодня температура воздуха на 20% выше, чем вчера. Обозначим температуру вчера как X. А сегодня как Y. Тогда Y = 0,2X + X = 1,2X.
 
Возникает вопрос, а для чего нужны математические модели? Как раз для того, чтобы мы могли решать разного рода задачи.


Использование математической модели для решения задач.

Пример задачи. У дяди Васи в саду 5 яблонь. 3 яблони с красными яблоками и 2 – с зелеными. Известно, что в среднем каждая яблоня с зелеными яблоками приносит в 2 раза больше килограмм яблок, чем яблоня с красными яблоками. Всего дядя Вася в итоге со всех деревьев собрал 35 кг яблок. Сколько в среднем приносит яблок яблоня с зелеными яблоками и сколько - с красными?  

Решение задачи. Для того чтобы ответить на поставленный вопрос, нам нужно составить математическую модель той ситуации, которая описывается в условии. Пусть X – количество килограмм красных яблок, которые может собрать дядя Вася с одной яблони. Тогда количество килограмм зеленых яблок, которые может собрать дядя Вася с одной яблони будет 2*X. Получаем следующее уравнение:

3*X + 2*(2*X) = 35.

3X + 4X = 35.

7X = 35

X = 35:7 = 5.

Получается, что в среднем дядя Вася с одной яблони с красными яблоками может собрать 5 кг. А зеленых соответственно 2*X = 2*5 = 10 кг.

Ответ: 5 и 10 кг.


Это лишь один пример из множества задач, которые помогают решить математические модели. По сути, для решения любой текстовой задачи, нам нужно выразить ее математическим языком, то есть составить математическую модель. Затем эту модель проработать (вычислить необходимые данные). И в итоге мы получим ответ на поставленный изначально вопрос.


Виды математических моделей.

Когда мы читаем условие текстовой задачи, мы имеем дело со словесной моделью задачи.
Затем, когда мы составляем уравнение для задачи, мы используем уже алгебраическую модель. Еще иногда нам требуется построить график по заданным данным. Это уже будет графическая модель (которую также можно назвать геометрической моделью). Все это виды математических моделей.
Хештеги: #алгебра :: #7 класс :: #математическая модель